射频/微波滤波器是几乎所有无线收发器设计的基本组成部分。滤波器在将带内信号传递到信号链的其余部分的同时,阻止应用工作带宽之外的不需要的信号。在高层次上,滤波器可以通过它们的响应来描述,即 S 21曲线在通带、过渡和阻带中的一般形状。理论上理想的滤波器将具有“砖墙”响应,在通带中表现出 0 dB 插入损耗,在频率截止 f c之外具有无限抑制,并在 0 Hz 时从通带过渡到阻带,如图 1 所示.
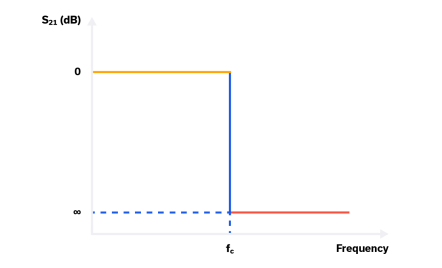
图 1:理想的滤波器传递函数。
实际上,射频滤波器受制于用于实现物理器件的电路拓扑结构的限制,以及其他因素,包括表面贴装 (SMT) 电容器的有限自谐振频率 (SRF)、有限品质因数 (Q ) 的 SMT 电感器,以及与用于容纳滤波器的印刷电路板 (PCB)、基板材料和封装相关的寄生效应。本简要指南将重点介绍用于设计射频滤波器的常用拓扑的基本性能特征,以及每种拓扑可以(和不能)支持的一般应用要求。
巴特沃斯滤波器(最大平坦或单调)
基于巴特沃斯多项式,对于给定的滤波器复杂度,该响应具有最平坦的通带响应。Butterworth 滤波器具有“最大平坦”的通带响应,这意味着它在通带中没有纹波。
随着巴特沃斯滤波器阶数的增加,过渡的锐度也随之增加,如图 2 所示。曲线 A 是一阶滤波器,每倍频程滚降为 6 dB,而曲线 B 是二阶滤波器。阶滤波器,每倍频程滚降 12 dB,依此类推。对于高阶滤波器,滚降为每倍频程 (6*N) dB,其中 N 是滤波器的阶数。Butterworth 滤波器结构可用于创建低通、高通、带通和带阻滤波器。
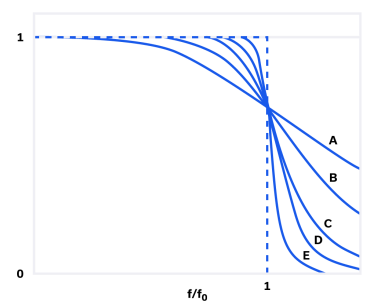
图 2:巴特沃斯滤波器频率响应作为滤波器阶数的函数。
尽管巴特沃斯的通带非常平坦,但它无法实现像下面讨论的其他一些滤波器拓扑那样陡峭的抑制曲线。为了实现“陡峭的裙边”,巴特沃斯滤波器必须是高阶的,这通常意味着牺牲通带中的插入损耗。
与大多数其他滤波器类型一样,巴特沃斯滤波器在通带中没有线性相位响应,尽管它们的相位响应比其他一些滤波器类型更线性。以每秒 1 弧度 (~0.16 Hz) 为中心的一阶巴特沃斯滤波器的相位响应如下图 3 所示:
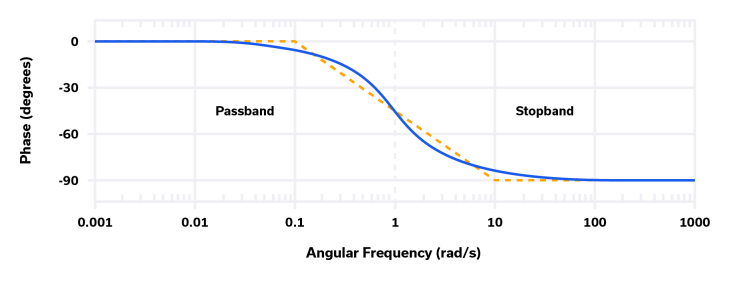
图 3:巴特沃斯滤波器在频率上的归一化相位响应。
任何在带内增益平坦度至关重要、需要过渡滚降和阻带抑制以及带内相位响应是次要问题的 RF 收发器都可以利用巴特沃斯滤波器的特性。Butterworth 滤波器也适合用作 ADC 中需要增益平坦度的抗混叠滤波器,并且对奈奎斯特区域之外的信号进行滤波可以防止由于混叠而引起的问题。
Chebyshev 滤波器类型 1(等波纹)
Type 1 Chebyshev 滤波器通常简称为“Chebyshev”,它基于 Chebyshev 多项式。它在通带中有一些纹波,但在阻带中表现出比巴特沃斯滤波器更陡峭的滚降和更高的衰减。与等效的巴特沃斯滤波器相比,它在通带中的插入损耗也更高。这可以从图 4 所示的切比雪夫滤波器频率响应中看出。切比雪夫滤波器的相位响应远非线性,如图 5 所示。
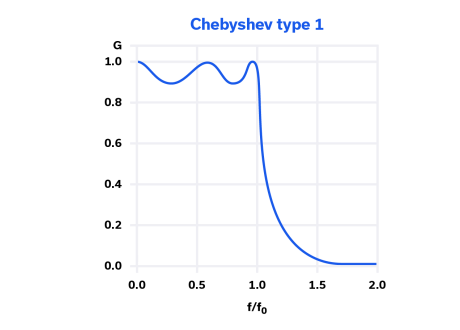
图 4:切比雪夫 1 型滤波器的频率响应。
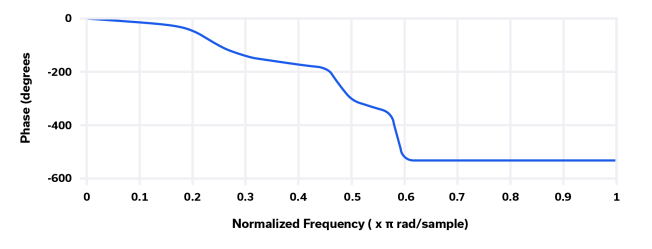
图 5:Chebyshev 1 型滤波器的归一化相位响应。
具有 Chebyshev 类型 1 特性的滤波器的典型应用是带内增益纹波是可接受的,但阻带滚降对于滤除带外杂散发射和其他类型的干扰至关重要。在天线处的 LNA 输入之前的接收器前端就是这样一个例子。
Chebyshev 滤波器类型 2(逆 Chebyshev)
Chebyshev Type 2 滤波器不如 Chebyshev Type 1 滤波器常见,因为它没有 Type 1 那样陡峭的滚降。它还需要比 Chebyshev Type 1 滤波器更多的元素来构建。然而,这种拓扑的好处是通过反转经典的切比雪夫响应,它消除了通带中的纹波。Chebyshev 2 型滤波器的传递函数如图 6 所示。图 7 所示的相位响应也很差。
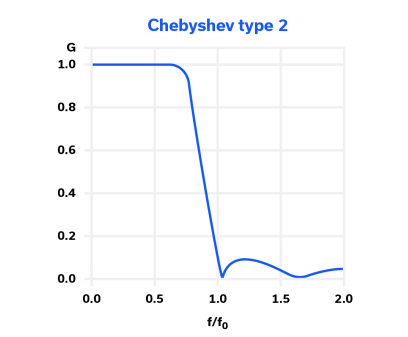
图 6:切比雪夫 2 型滤波器的频率响应。
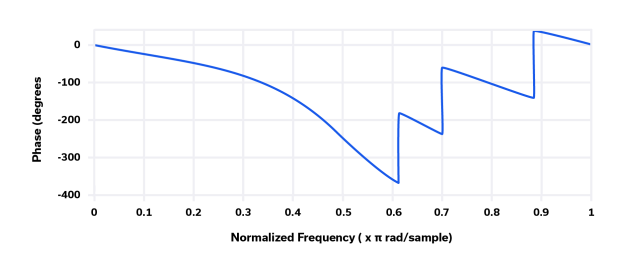
图 7:切比雪夫 2 型滤波器的归一化相位响应。
Chebyshev 2 型滤波器具有许多低频应用,例如桥式传感器和心电图 (EKG) 信号的滤波。
椭圆滤波器
椭圆滤波器响应(图 8)的特点是通带和阻带中的纹波相等,但通带和阻带中的纹波量是独立可调的。对于同阶滤波器,椭圆滤波器在此处讨论的所有拓扑中具有最陡的斜率,这使其适用于许多应用。实现这种类型的过滤器需要比 Chebyshev 1 型过滤器更多的元件,这使得设计和制造更加复杂和昂贵,但这可能是需要精确选择性的理想权衡。
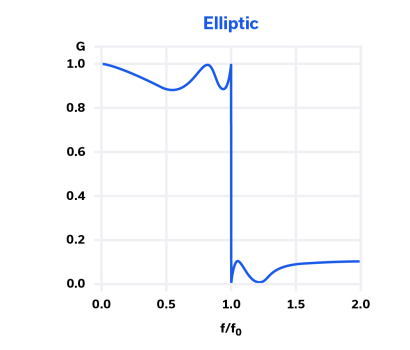
图 8:椭圆滤波器的频率响应。
椭圆滤波器的相位响应类似于 Chebyshev 1 型滤波器,因此对于需要恒定群延迟的应用来说并不理想。椭圆滤波器非常适合与宽带射频发射器中的功率放大器 (PA) 一起使用。滤波器特性支持 PA 在宽带宽上运行,同时在以最低频率运行时过滤 PA 的带外谐波。
贝塞尔滤波器(线性相位)
贝塞尔滤波器响应在所有常见拓扑中具有最平缓的斜率(最低选择性),如图 9 所示。然而,它的优势是在通带内具有最大平坦的群延迟。典型贝塞尔滤波器的群延迟与频率的关系如图 10 所示,定义为:
D = dΦ / dω
其中 Φ 是相移,ω 是角频率。群延迟是恒定的,贝塞尔滤波器的通带中的 D = 1,它最好地保留了从输入到输出的信号相位。
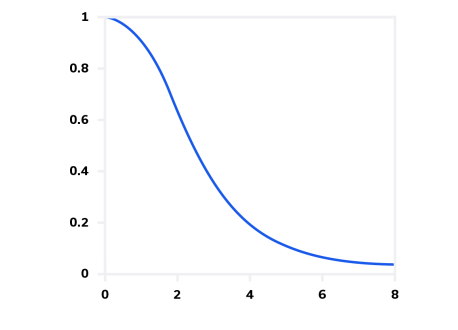
图 9:贝塞尔滤波器的频率响应。
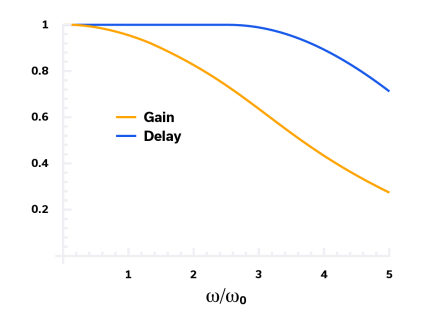
图 10:贝塞尔滤波器的群延迟。
贝塞尔滤波器用于模拟视频信号处理和音频交叉滤波等应用,将信号分成不重叠的多个频带。这些分离频带中的每一个的恒定群延迟是至关重要的。
Mini-Circuits 提供业界最广泛的射频/微波滤波器选择之一,包括展示此处描述的每种拓扑的模型。每个模型都提供了S 21曲线,您现在应该能够识别您的应用程序感兴趣的过滤器的不同响应类型。